What is Dynamic Programming? Understanding the Basics

Dynamic programming (DP) is a key technique in computer science and software development. It is well-known for efficiently solving complex problems by breaking them down into simpler problems. Richard Bellman introduced the term "dynamic programming" in the 1950s, and it has since become a cornerstone in algorithm design and optimization.

Why use dynamic programming?

When facing a problem involving a series of interconnected decisions, DP helps you find the solution step by step by using solutions to solve smaller subproblems. It's especially useful for problems that need optimization, decision-making, and resource allocation.

The benefits of dynamic programming include:

• Efficiency: It reduces time complexity by avoiding redundant calculations, allowing you to solve problems that would otherwise be computationally infeasible.
• Optimization: Ideal for finding the optimal solution among many possibilities, whether you’re maximizing profits, minimizing costs, or balancing resources.
• Versatility: Applicable to various domains, including artificial intelligence, machine learning, economics, bioinformatics, and operations research.
• Problem-solving: Encourages a systematic approach to breaking down complex problems into smaller, manageable parts and combining their solutions.
• Algorithm design: A fundamental technique in the design and optimization of algorithms, enhancing your ability to create efficient and effective solutions.

Tackling overlapping subproblems

You'll often face overlapping sub-problems in computer programming. These occur when you need to solve the same subproblems multiple times within a larger problem.

Dynamic programming helps to avoid this redundancy by solving each subproblem once and storing the result for future use, which is very useful when the same computations are repeated many times.

Approaches to dynamic programming

When it comes to dynamic programming, you’ll encounter two main approaches: the top-down approach and the bottom-up approach. Each method has its way of tackling problems and can be used based on the specific requirements of the problem at hand.

The top-down approach

The top-down approach starts by tackling the main problem and breaking it down into smaller, manageable subproblems. It relies heavily on recursion and memoization to store previously computed results and avoid redundant calculations.

Optimal substructure

The optimal substructure property indicates that an optimal solution to the problem can be constructed from optimal solutions of its subproblems. This characteristic is a fundamental reason why dynamic programming can be applied. Suppose you break down a problem into smaller, overlapping subproblems that can be solved independently and combined to form the solution to the larger problem. In that case, it means it possesses optimal substructure.

Many classic problems exhibit this property. For instance, take the shortest path problem. To find the shortest path between two nodes, you can use the shortest paths between intermediate nodes. Combining these shorter paths gives you the optimal path for the whole problem.

Recursive functions

Recursive functions are at the heart of the top-down approach in dynamic programming. Each recursive call tackles a smaller part of the problem until it reaches a simple base case. It’s easy to implement as it often aligns with the mathematical definition of a problem.

However, using a simple recursive algorithm can be inefficient, especially when the same subproblems are solved multiple times. For example, when calculating Fibonacci numbers with a straightforward recursive solution, the function fib(n) calls fib(n-1) and fib(n-2), which in turn call their own smaller subproblems. Doing so leads to many repeated calculations and can result in an exponential number of calls, which is very slow for large inputs.

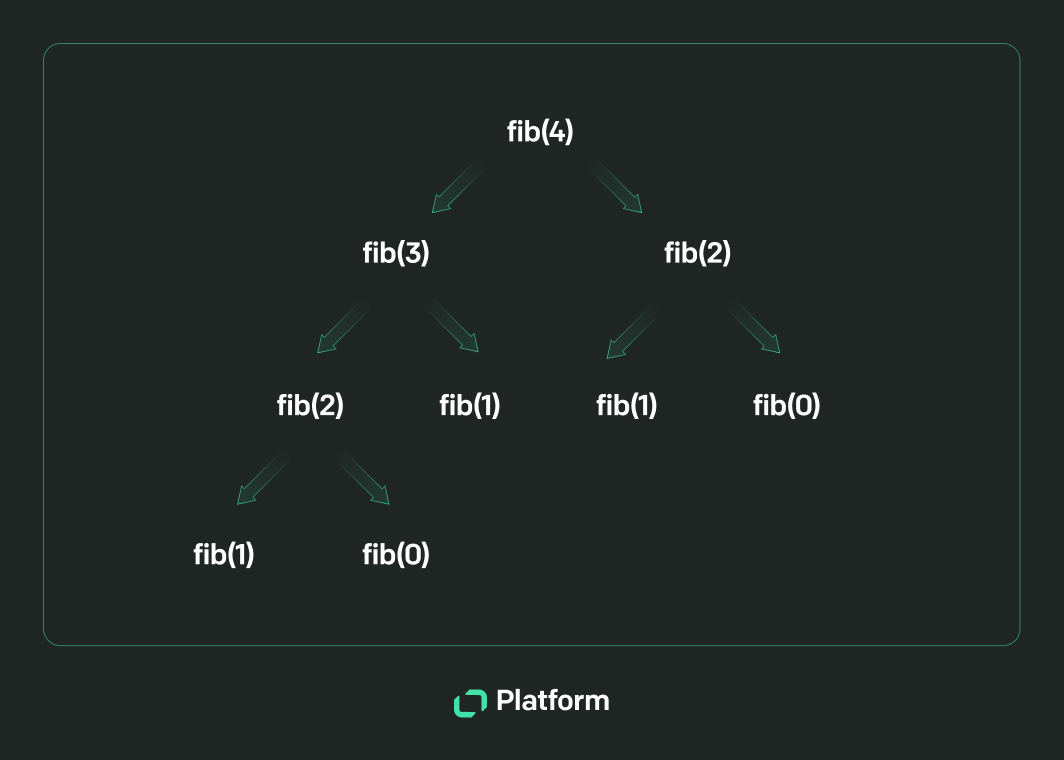
Memoization

To make recursive functions more efficient, you can use memoization. With this technique, you store solutions for expensive function calls in a cache and reuse these results when the same inputs occur again.

Memoization is key to improving the efficiency of the top-down approach by eliminating redundant calculations, which reduces the time complexity from exponential to polynomial. Depending on the specific problem and the nature of the subproblems, you can implement memoization using various data structures, such as dictionaries, arrays, or hash maps.

Top-down example

Let's look at the Fibonacci sequence to see how the top-down approach and memoization work in practice.

def fibonacci(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
    return memo[n]

In this example, the memo dictionary stores the results of Fibonacci computations. When fibonacci(n) is called, it first checks if the result for n is already in the memo dictionary. If it is, the function returns the cached result. If not, it computes the result, stores it in the dictionary, and then returns it, allowing each Fibonacci number to be computed only once, significantly improving efficiency.

Bottom-up approach

The bottom-up approach starts by solving the smallest subproblems first and then using their solutions to construct the solutions to larger subproblems. This method is also referred to as tabulation because it involves filling up a table based on previously computed values.

Tabulation

Tabulation has several advantages. Using an iterative algorithm with loops and arrays instead of recursion helps you avoid stack overflow errors. It's also more memory-efficient since you don't need to maintain a recursive function stack. Plus, the iterative solution is often easier to understand and debug compared to dealing with complicated recursive functions.

Bottom-up example

Let's now look at how the bottom-up approach works with the Fibonacci sequence:

def fibonacci(n):
    if n <= 1:
        return n
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i-1] + fib[i-2]
    return fib[n]

In this example, an array fib stores the computed Fibonacci numbers iteratively. The function initializes an array of size n+1 with all elements set to 0. It then sets the base cases fib[0] to 0 and fib[1] to 1. The function fills in the values of fib from index 2 to n using a loop, where each fib[i] is the sum of fib[i-1] and fib[i-2]. Finally, the function returns fib[n], which contains the n-th Fibonacci number.

Step-by-step example

Let's use the knapsack problem to illustrate how to use dynamic programming. Imagine you have a backpack that can hold up to 50 units of weight. You have three items with the following weights and values:

• Item 1: Weight = 10, Value = 60
• Item 2: Weight = 20, Value = 100
• Item 3: Weight = 30, Value = 120

You want to maximize the total value of the items in the backpack without exceeding the weight limit.

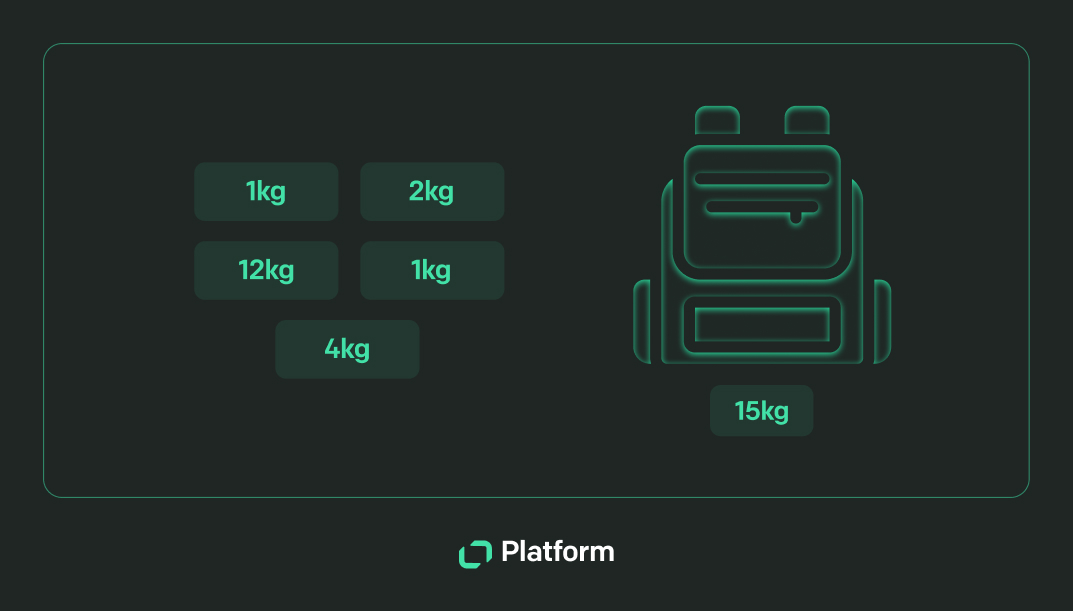
1. Break the problem into subproblems: For each item, consider two scenarios: including the item in the backpack or excluding it. Solve these subproblems to determine the maximum value achievable with and without the item.
2. Identify the base cases: If there are no items to consider, the maximum value is 0. If the weight limit is 0, the maximum value is also 0, as no items can be included.
3. Create a table to store results: Use a table to store the maximum value for each combination of items and weight limits. A dynamic programming table will help you avoid solving for previously calculated values.
4. Fill the table: Start with the base cases and fill the table by considering each item one by one. For each item, decide whether to include each item in the backpack based on its weight and value.
5. The final result: The maximum value you can achieve will be found in the last cell of the table.

The solution to this problem might look like this:

def knapsack(values, weights, max_weight):
    num_items = len(values)
    # Initialize the DP table with zeros
    dp = [[0 for _ in range(max_weight + 1)] for _ in range(num_items + 1)]

    # Build the table
    for i in range(1, num_items + 1):
        for w in range(max_weight + 1):
            if weights[i-1] <= w:
                # Include the item and check the value
                dp[i][w] = max(dp[i-1][w], dp[i-1][w-weights[i-1]] + values[i-1])
            else:
                # Exclude the item
                dp[i][w] = dp[i-1][w]

    # The maximum value is found in dp[num_items][max_weight]
    return dp[num_items][max_weight]

# Example usage:
values = [60, 100, 120]
weights = [10, 20, 30]
max_weight = 50
print("Maximum value in backpack:", knapsack(values, weights, max_weight))

This code builds a table (dp) where each entry dp[i][w] shows the maximum value you can achieve with the first i items and a weight limit w. By iterating through your items and deciding whether to include each one based on its weight and value, the code finds the maximum value you can fit into your backpack.

Best practices for implementing dynamic programming

To get the most out of your dynamic programming algorithms, keep these best practices in mind:

• Identify the recurrence relation: Start by figuring out the recurrence relation that defines your problem. This equation expresses the solution in terms of smaller subproblems.
• Choose the right data structure: Pick a suitable data structure to store solutions to the subproblems. Depending on your needs, you might use arrays, hash tables, or something more complex.
• Define the base cases: Clearly outline the simplest subproblems that can be solved directly. These base cases will stop the iteration or recursive function.
• Iterate or recur efficiently: Depending on your approach, either iterate through the problem space or use recursion to build up the solution. Make sure to solve subproblems in an order that respects all dependencies.
• Analyze time and space complexity: Evaluate how much time and memory your solution needs. Dynamic programming can save time but might use more memory because it stores solutions to subproblems. Find a balance that works best for your specific problem.

Advanced concepts and techniques

To harness the power of dynamic programming and solve challenging problems when writing computer code, you'll want to explore some advanced concepts and techniques.

State space

State space refers to all the possible states or configurations of your problem. Optimizing this space directly impacts the memory and time your solution will need. You can make your state space smaller by cutting out unnecessary states. For instance, in sequence problems, focus only on the necessary subsequences instead of considering all possible ones.

Bitmasking

Bitmasking helps you represent the state space compactly, especially in combinatorial problems. It uses binary numbers to efficiently represent subsets of elements. Each bit in a binary number corresponds to an element, where a bit value of 1 means the element is included, and 0 means it's not. For example, if you have a set of four elements, the binary number 1010 would represent a subset, including the first and third elements.

Let's consider the traveling salesman problem (TSP), a classic example of mathematical optimization, where you need to find the shortest possible route that visits each city exactly once and returns to the starting city. You can use bitmasking to represent the set of visited cities:

def tsp(mask, pos, dp, dist):
    if mask == (1 << len(dist)) - 1:
        return dist[pos][0]

    if dp[mask][pos] != -1:
        return dp[mask][pos]

    ans = float('inf')
    for city in range(len(dist)):
        if mask & (1 << city) == 0:
            new_ans = dist[pos][city] + tsp(mask | (1 << city), city, dp, dist)
            ans = min(ans, new_ans)

    dp[mask][pos] = ans
    return ans

# Example usage:
n = 4
dist = [
    [0, 10, 15, 20],
    [10, 0, 35, 25],
    [15, 35, 0, 30],
    [20, 25, 30, 0]
]

dp = [[-1] * n for _ in range(1 << n)]
result = tsp(1, 0, dp, dist)
print("The shortest path length is:", result)

In this example, mask is a bitmask representing the set of visited cities, and pos is the current position. The dist matrix contains the distances between the cities, and dp is the memoization table that stores the minimum distance for each state. The function tsp recursively calculates the shortest path using bitmasking to keep track of the visited cities.

Hash map memoization

Hash map memoization is useful when the state space is sparse or irregular. Using a hash map (or dictionary) for memoization can save memory compared to using arrays. This method stores only the states that have been encountered, which is more memory-efficient; however, it might slightly increase retrieval time.

Rolling hashes and hash collisions

Rolling hashes and hash collisions are useful for problems involving strings or sequences. Rolling hashes generate unique keys for states, which reduces the risk of hash collisions. A hash collision occurs when two different inputs produce the same hash value, causing errors in your program as it may mistakenly treat different inputs as the same. It’s also a great method when you need a reliable way to compare sections of text.

Let's combine both concepts in a problem where you need to find the longest repeated substring in a given string. We'll use rolling hashes to generate unique keys for substrings and hash map memoization to store and compare these substrings:

def rolling_hash(s, base=256, mod=101):
    hash_value = 0
    for char in s:
        hash_value = (hash_value * base + ord(char)) % mod
    return hash_value

def update_hash(old_hash, old_char, new_char, base, mod, base_m):
    new_hash = (old_hash * base - ord(old_char) * base_m + ord(new_char)) % mod
    return (new_hash + mod) % mod  # Ensure non-negative

def longest_repeated_substring(text):
    n = len(text)
    base = 256
    mod = 10**9 + 7  # A larger prime number to reduce collisions
    max_len = 0
    result = ""

    for length in range(1, n):
        hash_map = {}
        current_hash = rolling_hash(text[:length], base, mod)
        base_m = pow(base, length - 1, mod)  # base^(length-1) % mod

        hash_map[current_hash] = [0]

        found = False
        for i in range(1, n - length + 1):
            current_hash = update_hash(current_hash, text[i - 1], text[i + length - 1], base, mod, base_m)
            if current_hash in hash_map:
                for start in hash_map[current_hash]:
                    if text[start:start + length] == text[i:i + length]:
                        found = True
                        if length > max_len:
                            max_len = length
                            result = text[i:i + length]
                        break
                if found:
                    break
            else:
                hash_map[current_hash] = [i]

        if not found:
            break

    return result

# Example usage:
text = "banana"
print("Longest repeated substring:", longest_repeated_substring(text))  # Output: "an"

Problems that aren't a good fit for dynamic programming

Not all problems are dynamic programming problems. For DP to work well, a problem must have an optimal substructure and overlapping subproblems.

For instance, divide-and-conquer methods are better for problems involving independent subproblems, where each part can be solved independently without reusing previous results. Also, problems that need real-time decisions based on constantly changing inputs, like certain real-time systems or dynamic environments, lend themselves poorly to a dynamic programming approach.

Real-life examples include:

• Mergesort and quicksort algorithms use a divide-and-conquer approach, breaking the problem into independent subproblems.
• Real-time stock trading requires rapid decision-making based on constantly changing market conditions.
• Self-driving cars need to make immediate decisions based on dynamic environments.
• Online algorithms for caching or streaming data processing make decisions without knowing future inputs. For an efficient approach, you’d need algorithms that can adapt on the fly, reacting to new data as it arrives.

Classic problems solved by dynamic programming

Dynamic programming is a powerful and flexible approach to solving various complex problems efficiently. Let's cover some classic dynamic programming problems and their applications.

1. Optimization problems

Optimization problems require finding the best solution among many possibilities. These problems are often about maximizing or minimizing a particular value.

Let’s reconsider the knapsack problem, where you are packing a bag with items, each having a weight and a value. You need to determine which items to include so that the total weight is within a limit and the total value is maximized. Here, a cost function helps evaluate the value and weight of the items to achieve the optimal solution. A similar scenario can apply to budget allocation, resource management, and project selection.

And remember the traveling salesman problem? Dynamic programming works here to find the shortest possible route that visits each city exactly once and returns to the starting point. Solving this problem is crucial in logistics, route planning, and network design. It's heavily used by shipping companies and retailers like Amazon to optimize delivery routes.

2. Combinatorial problems

Combinatorial problems involve combinations and arrangements of items. These problems often focus on counting or enumerating possible arrangements.

For instance, counting subsets involves determining the number of subsets of a set that sum to a given value, which can be useful inbpartitioning tasks among employees or dividing resources. Another example is finding the longest common subsequence in two sequences, which is helpful in DNA sequence analysis, text comparison, and version control systems.

3. String processing

String processing problems involve manipulating and analyzing text strings. These problems can range from simple modifications to complex pattern recognition.

The edit distance problem, also known as Levenshtein distance, involves finding the minimum number of operations (insertions, deletions, or substitutions) required to transform one string into another. You could use this in spell-checking, text correction, and natural language processing (NLP).

Pattern matching involves finding all occurrences of a pattern string within a larger text. It plays a crucial role in search algorithms for quickly locating information, plagiarism detection for identifying copied content, and bioinformatics for matching DNA or protein sequences.

4. Game theory

Game theory focuses on finding the best strategies for players, considering the possible moves and outcomes in competitive situations.

The minimax algorithm is used in two-player games like chess or tic-tac-toe and seeks to minimize a player's maximum possible loss. Such a mechanism is integral to AI for games and formulating competitive strategies in various fields.

In zero-sum games, where one player's gain is another's loss, dynamic programming helps analyze strategies and determine optimal plays, valuable in:

• Economics for market competition
• Politics for election strategies
• Military strategy for conflict simulations

5. Computer graphics and robotics

In computer graphics and robotics, matrix chain multiplication is frequently used for transformations, including rotation, scaling, and translation. Determining the optimal order of matrix multiplications can reduce the computational overhead, leading to faster and more responsive graphics rendering in animations, simulations, and robotic movements.

6. Financial systems and vending machines

The coin change problem is directly applicable to systems that handle cash transactions, such as vending machines, ATMs, and cashier systems. In these systems, it's important to give the fewest coins or notes as change to avoid frequent coin restocking.

Real-world applications in software development

If you’re still not sure how you can use dynamic programming in your projects, here are some practical applications that demonstrate its power and versatility:

• Resource allocation: Provides an optimization technique for allocating resources like memory and CPU cycles. For instance, in cloud computing, dynamic programming can allocate virtual machines to tasks in a way that minimizes costs while meeting performance requirements.
• Scheduling problems: Provides solutions for job scheduling with deadlines, minimizing total completion time, or maximizing resource utilization in real-time and embedded systems.
• Data compression: Achieves optimal compression rates for images and videos by determining the best way to encode data, reducing file sizes without compromising quality.
• Network routing: Determines the most efficient route for data packets using algorithms like Bellman-Ford, optimizing network traffic and ensuring reliable data transmission.
• Machine learning and AI: Solves complex decision-making problems in reinforcement learning by computing value functions that guide intelligent agent behavior.
• Real-time systems: Handles immediate responses to changing conditions by precomputing and storing solutions for quick access, such as in robotics for optimal path planning.
• Text processing and analysis: Used in NLP for text segmentation, parsing, and machine translation by finding the most likely sequence of words or phonemes.

Use cases and benefits in the Text Platform

If you want to enhance your communication solutions, the Text Platform offers a suite of APIs and SDKs to take your applications to the next level. Dynamic programming can significantly improve various aspects of these solutions.

1. Optimizing message parsing and analysis

You might need efficient message parsing and analysis algorithms when building chat applications using the Text Platform's advanced API collection. For example, you could use dynamic programming to create a spam filter that categorizes messages based on their content.

By breaking down the problem into smaller tasks, such as tokenizing the message, checking for spam patterns, and storing the results, you can develop a system that quickly and efficiently filters out unwanted messages.

2. Optimizing API calls and data processing

Using the Text Platform’s APIs for chat messaging and data reporting, you can apply dynamic programming to optimize the frequency and efficiency of API calls. Caching and reusing the results of expensive API calls can reduce the number of calls made, saving bandwidth and improving response times.

3. Building intelligent chatbots

Chatbots are an integral part of many applications built on the Text Platform. Dynamic programming can help develop intelligent chatbots that understand and respond to user queries. Techniques like NLP and dynamic decision trees can enhance your chatbot’s ability to provide accurate and relevant responses.

With the Text Platform's Open Chat Widget, you can seamlessly integrate these advanced chatbots into your applications, delivering a smooth and engaging user experience.

4. Custom reporting and analytics

The Text Platform’s APIs offer extensive capabilities for data reporting and analytics. You can use DP to build custom analytics tools that process large datasets. For example, a developer could implement a dynamic programming algorithm to generate real-time sentiment analysis reports from chat logs, providing valuable insights into customer satisfaction.

The Text Platform empowers developers

The Text Platform is your gateway to expanding your reach and monetizing your products on external marketplaces. Here’s how we support developers like you:

• Our extensive range of APIs and SDKs for chat messaging, reports, and configuration allows you to extend or integrate our products with your solutions.
• We provide APIs for various text operations, giving you a solid foundation to build your unique solutions.
• Publish your apps on the Text Marketplace and explore various passive income streams.
• Gain instant access to a ready customer base by listing your app on the Text Marketplace.
• Elevate LiveChat and HelpDesk tools with your apps.

We hope you've discovered new ways to incorporate dynamic programming into your projects using the Text Platform.

Whether you’re building intelligent chatbots, optimizing API performance, or creating powerful analytics tools, dynamic programming can help you develop more efficient and impactful solutions.