What you’ll learn from this article:
- How binary code represents data
- Where binary numbers come from and their historical context
- How binary compares to the decimal system
- What binary-coded decimal is and how it’s used
tl;dr
Binary code is the system of 1s and 0s that computers use to represent information.
So, what is binary code?
Binary is the simplest numeric system, using only two digits: 0 and 1. Computers rely on it because it’s easy to translate into electrical signals, on and off. Every image, file, app, or sound you use is stored and processed as binary under the hood.
Key findings
Why do computers use binary and not something more complex?
Binary is extremely reliable and efficient for machines to process. It aligns with electrical circuits that have two states: on and off.
Do developers need to know binary?
You don’t have to write in binary daily, but understanding it helps with data representation, bitwise operations, and low-level debugging.
How does binary show up in programming?
Binary is at the heart of everything — from encoding characters in UTF-8 to defining pixel colors or doing binary logic in conditional checks. You’ll see it when working with permissions, networking, or embedded systems.
Read on if you're still interested in more details about binary!
In computer systems, only two numbers are used: 0 and 1. That's a binary number system.
It can be quite hard to understand how computing systems can process all the data using just two binary number systems. This guide will act as a bridge to the high-level language and binary code.
Let's start with the definition.
What is binary code?
Binary code is the most basic form of data representation in computer systems, as well as digital systems. It consists of just two decimal digits—0 and 1.
In short, a binary contains only those two digits, while the binary code is a series of these digits.
Now, let’s get a little technical and understand the concept in depth: bits and bytes are two important concepts you need to know about binary systems.
Bits refer to binary digits—the foundational elements of the binary numbering system. A binary digit can only have one of the two possible values, 0 or 1. Binary bits are usually used to represent a state in an electronic device, such as on/off or true/false, where 1 is usually on/true and 0 is off/false.
In the same way, a byte is a larger unit of the data that combines eight bits. Bytes are the standard unit for measuring storage size. A single byte can represent 256 different values (2^8 = 256). So, a byte (if converted to binary numbers) can range from 00000000 to 11111111.
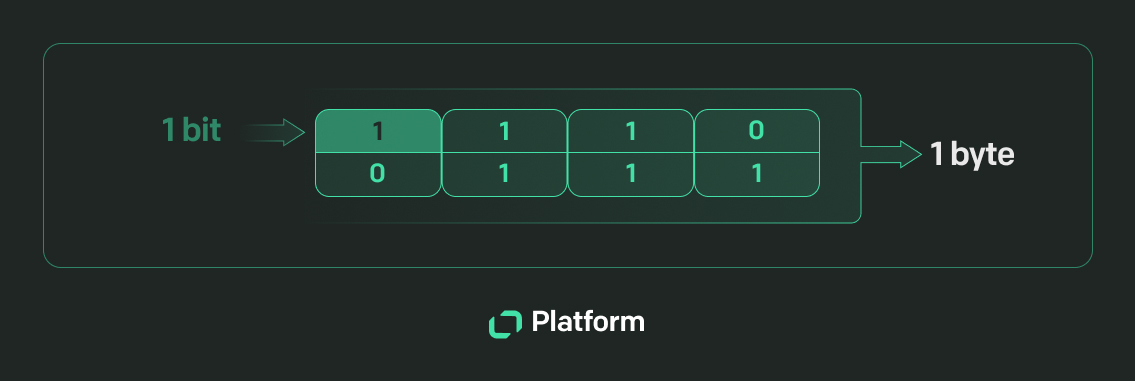
Just like humans use English to communicate, computers communicate in binary formats. The programming languages you use, such as Python, R, etc., are converted into binary code.
Short history of binary codes
The origins of binary concepts can be traced back to ancient ideas of duality, such as the yin-yang philosophy in China and Pingala’s work on binary representations in India. The I Ching’s hexagrams are an early example of binary patterns.
Building on these foundations, Gottfried Wilhelm Leibniz formalized binary as a mathematical number system. Later, Francis Bacon used binary to encode text, laying the groundwork for modern data representation, while pioneers like George Stibitz and Konrad Zuse advanced binary’s application in early computing.
Binary also found practical use in communication technologies, with devices like the Linotype machine and Baudot’s telegraphy system. Further innovations, including binary-coded slide rails and the Excess-3 code, played a crucial role in shaping the evolution of digital technology.
Binary system vs. decimal system
A binary system operates with two binary digits, 0 and 1, while the decimal system uses all the decimal numbers (0 to 1). It’s easier for computers to calculate and perform operations in two numbers instead of using decimal values.
Binary code is used to represent numbers in computing systems, utilizing 1s and 0s to encode numerical values as electrical signals.
Decimal values can easily be converted to binary values. To get a binary code for a decimal value, you need to divide the decimal number by 2 and take note of the remainder. Then, write the remainders in reverse order to get the binary number.
Let’s take an example of 13:
- 13 ÷ 2 = 6 remainder 1
- 6 ÷ 2 = 3 remainder 0
- 3 ÷ = 1 remainder 1
- 1 ÷ = 0 remainder 1
Now, write the remainders from bottom to top: 1101. This is the binary value of 13.
The rightmost digit in this binary value represents the smallest power of 2 ( 2^0 ), just as the rightmost digit in a decimal number represents the smallest power of 10.
Why does this work?
Each remainder represents whether a specific power of 2 is “on” (1) or “off” (0). When we read the remainders from the bottom up:
- The rightmost digit represents 2^0 (1).
- The next digit to the left represents 2^1 (2).
- The next represents 2^2 (4).
- The leftmost digit represents 2^3 (8).
Adding these powers of 2 gives us back our original number: 8 + 4 + 0 + 1 = 13.
Looks easy, right? You might be wondering, if we already have the binary numbers converted from the decimal number, why don’t we use the same binary data instead of doing the binary arithmetic? That’s where binary-coded decimal (BCD) comes into the picture.
Binary-coded decimal
Binary-coded decimal is where each of the binary numbers is directly represented as binary digits. For instance, the binary code of 9 is 1001, and 3 is 0011. So, the BCD of 93 is represented as 1001 0011.
It saves you a lot of time as the fixed binary number system helps the computer systems to make faster calculations. It’s commonly used in digital clocks, calculators, integrated oscillators, and similar applications where accuracy is important.
You might think that BCD arithmetic and pure binary are the same. However, they're not.
- The pure binary of 93 is 1011101.
- The BCD arithmetic of 93 is 1001 0011.
So, pure binary uses less memory compared to BCD.
Both arithmetic operations have different use cases. Binary arithmetic is more efficient whereas BCD arithmetic operations are used when there is a need to preserve the value of each digit. As BCD saves the value of each numerical value separately, it's highly suitable for financial operations.
Types of binary codes
There are multiple types of binary codes for different purposes. We will learn about each type of binary code in detail.
ASCII codes
American Standard Code for Information Interchange (ASCII) is a character encoding standard that uses 7 or 8 bits to represent characters. Each of these characters can be a letter, number, or symbol. Each are assigned a unique binary number.
Each character in the ASCII table corresponds to an associated decimal value, enabling applications to read and store text information in computer memory.
For example, the ASCII code for A is 65, which is 1000001 in binary. ASCII-capable applications include data transmission, computer programming, telecommunication, etc.
Unicode
Unicode is an extension of ASCII codes to support more characters. It also includes multiple encoding forms including UTF-8, UTF-16, and UTF-32. UTF-8 uses 8-bit blocks and so on. While ASCII codes have limited support for characters, Unicode includes characters from all languages and devices, including numerals, punctuation marks, symbols, and emoji. You can view Unicode charts on dedicated websites.

Error detection code
Electronic devices can encounter problems in data transmission, so an error detection code is important. In modern computers, parity bits and checksums are the two codes used to check error detection. During the transmission, an extra (1-bit) parity bit (even or odd) is matched. If they fail to match, an error is detected in the transmission.
Understanding important binary code concepts
Binary code is a huge topic. Your computer understands everything in binary numbers only. For this reason, understanding the entire binary number system will take a lot of time.
We have crafted this section to briefly explain all the important concepts.
How is text represented in binary code?
Text representation in binary code is done by ASCII and Unicode. Each character is converted to a binary sequence. For example, A is 01000001 in ASCII, and あ in UTF-8 is 11100011 10000010 10100010.
What is a binary shift operation?
Binary shift operations move bits left or right within a binary number. For instance, in arithmetic operations, the binary shift operation is used in dividing or multiplying by the powers of 2.
How are binary numbers represented and used?
Binary numbers are represented using the digits 0 and 1. This is how binary numbers help with all electronic operations.
In computing, code is often translated into binary format for execution by computers, highlighting its fundamental role in digital communication and the representation of information.
- Digital electronics: Representing on/off states in circuits.
- Computing: Storing and processing all forms of data.
- Communications: Encoding data for transmission over networks.
What is binary code optimization?
Binary code optimization is the process of simplifying the code for faster execution. Multiple methods are used for binary code optimization, such as code reordering, loop unrolling, and instruction selection. In the same way, computer systems use methods like Huffman coding for data compression.
Converting modern languages to binary code
Now that you have a better idea of binary code and binary numbers, we will talk about how modern-day language is converted to binary.
Developers used to code in assembly language, which involved a lot of code. As technology evolved and computer science made great progress, easy-to-write high-level programming languages were introduced.
In a high-level language, you get the desired output with just a few lines of code.
Some third-party APIs make the coding extremely simple. For instance, there were previously many dependencies on multiple technologies. If you wanted to make a simple tracking application that tracks reports and generates charts, you would have to integrate many libraries and technologies.
However, modern platforms such as Text provide everything under one roof. Text has everything you need to start developing your apps. It's suitable for junior and senior developers.
You can even publish the app on the Marketplace once the app is developed.
Now, let's get back to the basics and understand how computing systems understand your code.
High-level language to binary code
When you write code in any desired language, the code is first either complied using a compiler or interpreted using an interpreter. The compiler and interpreter convert the human-readable language into a machine-level language.
So, when you write a simple hello world code in Python or any other language, there are multiple steps followed to convert the code into binary.
- Lexical analysis: The compiler reads the source code and breaks it into tokens. Tokens are the smallest unit of code.
- Syntax analysis: The compiler checks the tokens against the syntax. For instance, if the "print" is misspelled, it shows an error.
- Semantic analysis: The compiler checks for semantic errors. These are also called logical errors. For example, a type conversion error is one example of a semantic error.
- Optimization: Before it's sent to the final level, the compiler will optimize the code to save memory and for faster execution.
- Code generation: The compiler generates the machine code (binary code) that the computer’s processor can execute.
Applications of binary code
Binary code is fundamental to modern technology, enabling everything from basic calculations to advanced data processing. It drives decision-making and counting in circuits through Boolean algebraic operations and binary counters. Analog signals are converted into binary for seamless digital processing, forming the backbone of modern computing. Cryptographic algorithms use binary to secure data, while binary-based compression algorithms optimize storage and transmission.
Binary also powers essential technologies like digital clocks, computers, and media processing systems. File compression formats rely on binary to save space, and machine code — comprised of binary instructions — is directly executed by processors. At the core of all digital electronics are transistors, which represent binary states and make the entire digital world possible.
Other forms of binary code
The concept of binary extends beyond technology into cultural and symbolic systems. For instance, Braille uses a tactile binary system, where raised or unraised dots form characters that convey written language.
Similarly, traditional practices like geomancy, Ifá, and Ilm al-Raml rely on binary-like patterns to interpret meanings and make predictions. The I Ching, with its hexagrams, represents one of the earliest examples of binary arrangements, reflecting ancient understandings of duality and order. These applications highlight the adaptability of binary principles across cultural traditions and technological advancements.
Conclusion
Binary code is the core language of computer systems using only 0 and 1. A series of both these numbers are used to convert the primary language into binary.
However, binary language is only for computers. While it's good to have basic knowledge about the binary form of data, there isn't a major practical use for it. Modern computer systems work on high-level languages, such as Python or Java, and platforms like Text help developers build apps. So, you don’t have to know binary by heart to be a good developer.


